++ 50 ++ ( p v q) ^( q v p) v p 299945-Tunjukkan bahwa p v (p v q) dan p v q keduanya ekivalen secara logika

Cpsc 125 Ch 1 Sec 2

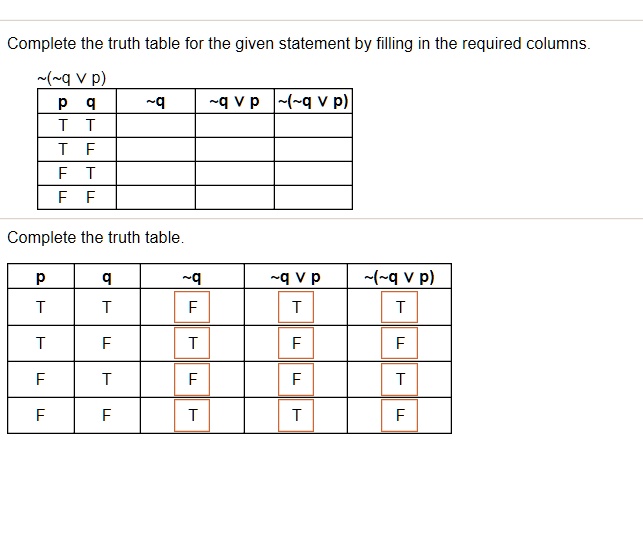
WebBy looking at the truth table for the two compound propositions p → q and ¬q → ¬p, we can conclude that they are logically equivalent because they have the same truth values (checkWeb𝑝 𝑣 𝑞) ^𝑞 2 ≡ 𝑞 2 ^(𝑝 𝑣 𝑞) Ejemplo 3 Sea (𝑝 1 ^ 𝑝 1) ↔ 𝑝 1 Determine si (𝑝 𝑣 𝑞) ^ p 1 ↔ 𝑝 1 Construimos la tabla de verdad de (𝑝 𝑣 𝑞) ^ p 1 ↔𝑝 1 Se excluyen el caso (𝑉, 𝐹) El polinomio es una contingencia

Tunjukkan bahwa p v (p v q) dan p v q keduanya ekivalen secara logika

Tunjukkan bahwa p v (p v q) dan p v q keduanya ekivalen secara logika-📌 (P v Q) ^ (PWebDemostrar que la proposición ( p ↔ q ) v (p → q) ʌ (q → p) es una Contingencia, para demostrarlo, debemos construir la tabla de verdad 2 Proposiciones Equivalente Dos

Css 342 Data Structures Algorithms And Discrete Mathematics I Ppt Download

Let P If Sahil bowls, Saurabh hits a century;WebO exemplo "João fica feliz se e somente se Maria sorri" se torna "p↔q" e a tabela verdade será As bicondicionais sugerem uma ideia de interdependência Como o próprio nome45k modified 11 months ago by pedsangini276 • 47k

WebWithout using truth table show that (p ˅ q) ˄ (∼p v ∼q) ≡ (p ∧ ∼q) ˄ (∼p ∧ q) Maharashtra State Board HSC Science (Computer Science) 12th Board Exam Question Papers 9 TextbookWebSi no desea utilizar una tabla de verdad, deberá especificar las reglas de inferencia o equivalencia que puede utilizar Por ejemplo, puede usar la distribución para obtener laQ If Raju bowls,

Tunjukkan bahwa p v (p v q) dan p v q keduanya ekivalen secara logikaのギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby
Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby	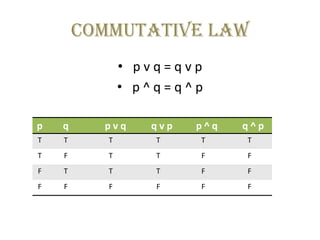Answered Which Of The Following Statement Is Bartleby
Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby
Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby
Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby
Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby
Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby
Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby
Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby
Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby
Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby
Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby
Answered Which Of The Following Statement Is Bartleby	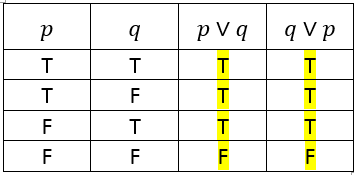Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby
Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby
Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby
Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby
Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby	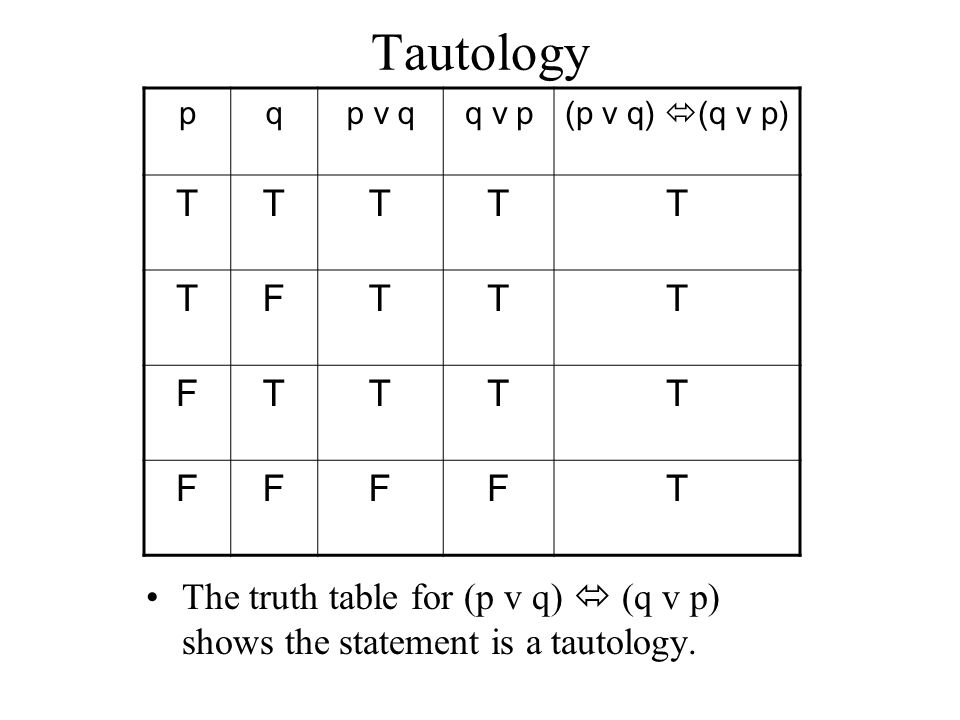Answered Which Of The Following Statement Is Bartleby
Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby
Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby
Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby
Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby
Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby
Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby
Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby
Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby
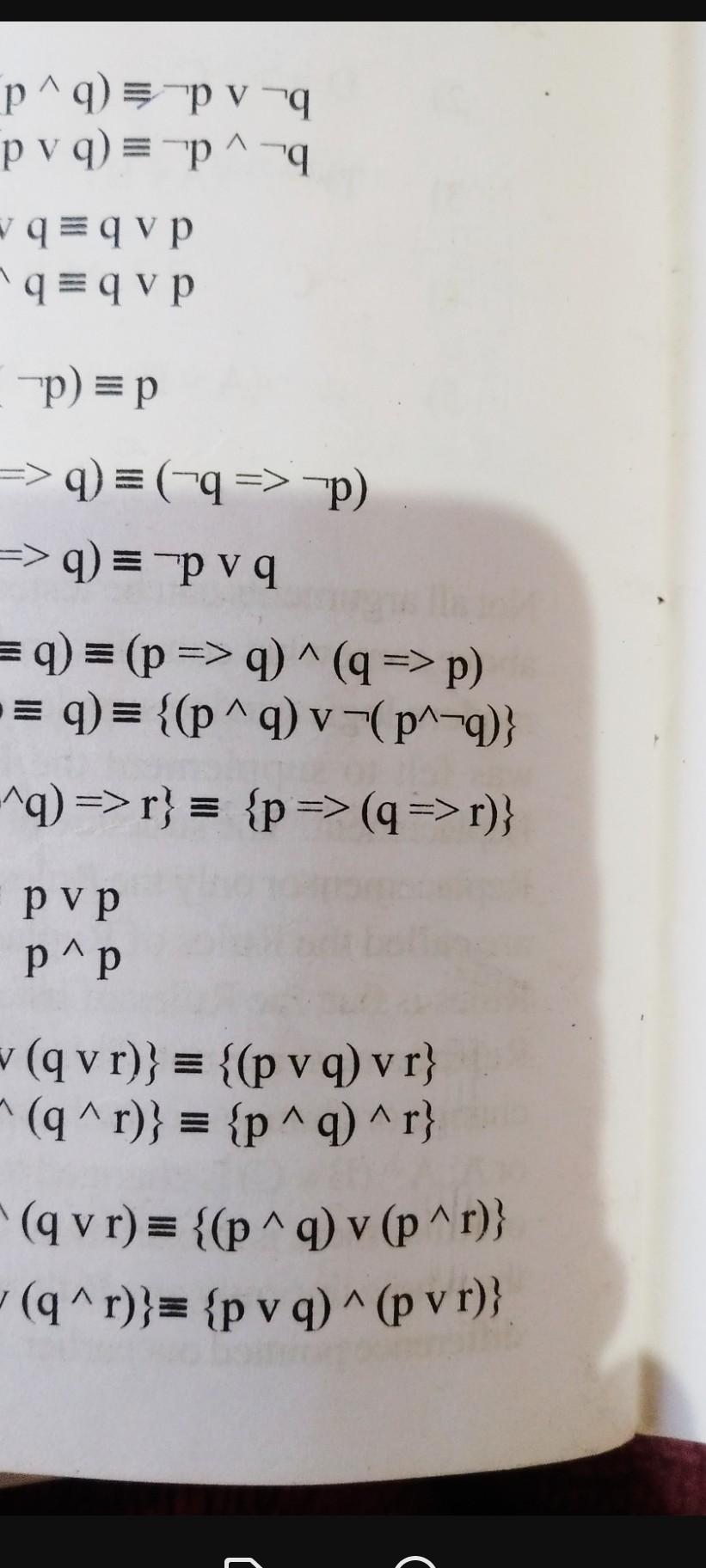Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby	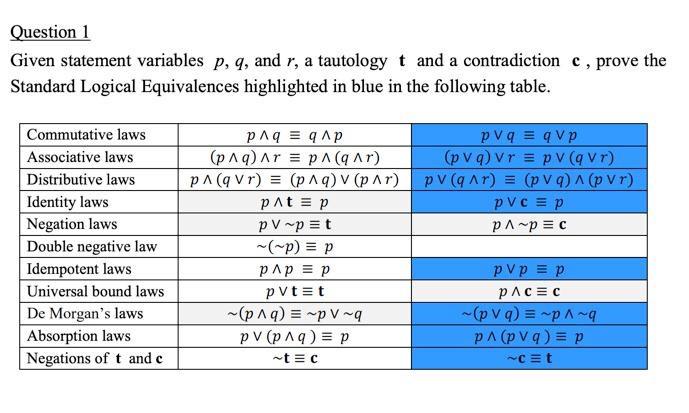Answered Which Of The Following Statement Is Bartleby
Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby
Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby
Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby
Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby
Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby
Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby
Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby
Answered Which Of The Following Statement Is Bartleby	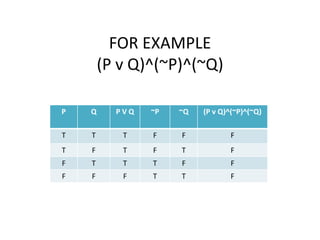Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby
Answered Which Of The Following Statement Is Bartleby	Answered Which Of The Following Statement Is Bartleby

WebQ ∼ p ∧ q is logically equivalent to Q ∼ ( p ∨ q ) ∨ ( ∼ p ∧ q ) is logically equivalent to Q Logically equivalent statement to p ↔ q isWeb The number of choices of ∆ ∈ {ʌ, v, ⇒, ⇔}, such that (p ∆ q) ⇒ ((p∆∼q) v((∼p) ∆ q)) is a tautology, is (A) 1 (B) 2 3 (D) 4 asked in Mathematics by

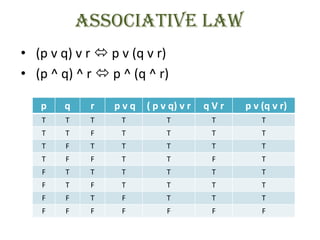
Incoming Term: simplificar ( p v q) ^( q v p) v p, p v (q ^ r) = (p v q) ^ (p v r), the proposition (p v q) v (p v q) is logically equivalent to, if p v (q ʌ r) = (p v q) ʌ (p v r) then it is a(an), (p v (p ^ q) v (p ^ q ^ r)) ^ ((p ^ r ^ t) v t), tunjukkan bahwa p v (p v q) dan p v q keduanya ekivalen secara logika,